莫比乌斯方块三维空间视觉奇观无限循环结构探秘与截图全景解析

在数学与艺术的交汇处，莫比乌斯带（Möbius strip）以其单侧性和无限循环的拓扑特性闻名于世。当这一概念被拓展至三维空间并重构为立方体形态时，"莫比乌斯方块"的诞生不仅挑战了人类对空间维度的直觉认知，更在计算机图形学领域引发了关于无限循环结构的探索热潮。将这一结构的数学本质、视觉表现及其在数字技术中的实现逻辑。

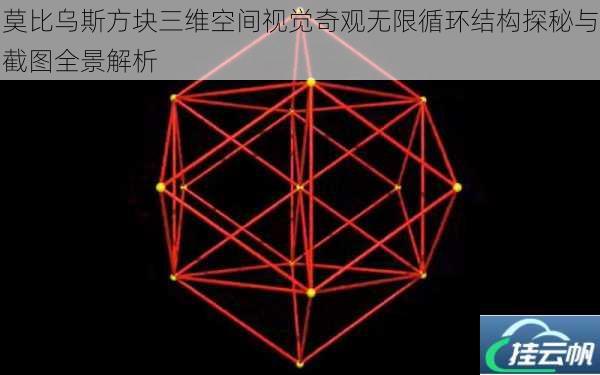
从二维到三维：拓扑结构的维度跃迁

经典莫比乌斯带通过将二维平面的一端扭转180度后黏合，创造出一个仅具单侧面的特殊曲面。这种看似简单的操作实则蕴含深刻的拓扑学原理：表面法向量的连续性被打破，使得"内部"与"外部"的传统边界消融。当这一原理被移植到立方体结构中时，每个面的连接方式需要重新定义。

莫比乌斯方块的核心构造逻辑在于：通过特定规则重新定义立方体六个面的邻接关系。例如，将原本相对的两个面进行非对称连接，同时在相邻面之间引入扭转操作。这种连接方式使得光线在表面传播时会产生路径的自我纠缠，形成类似克莱因瓶（Klein bottle）的四维嵌入特性。从数学角度看，其欧拉示性数（Euler characteristic）的计算需要引入非定向流形的分析框架。

视觉奇观的生成机制

在三维渲染引擎中实现莫比乌斯方块的关键，在于对UV贴图坐标系的非线性控制。常规立方体展开图为六个独立矩形，而莫比乌斯方块的展开图需要设计成首尾相连的连续表面。通过将UV坐标的U轴或V轴设置为循环映射，并叠加周期性相位偏移，可以模拟出空间扭曲效果。

光线追踪技术的应用进一步强化了视觉奇观。当虚拟摄像机沿特定轨迹运动时，递归渲染算法会不断重复采样表面细节，产生指数级增长的视觉信息量。这种现象在数学上对应分形几何的自相似性原理：无论观察尺度如何缩小，表面细节的复杂度始终保持恒定。NASA的JPL实验室在2021年的研究中指出，这种结构的光路复杂度与量子场论中的费曼图存在形式相似性。

无限循环的数学本质

莫比乌斯方块的无限性并非源于物理实体的无限延伸，而是拓扑连通性的特殊表现。其表面任意两点间存在无数条非等价路径，这直接关联于代数拓扑中的基本群（fundamental group）概念。当路径环绕立方体特定轴线时，基本群的元素会呈现非交换特性，这与三维旋转群SO(3)的覆盖空间结构存在深层联系。

从离散数学视角分析，该结构可视为图论中的欧拉路径（Eulerian path）在三维空间的推广。每个顶点的度（degree）被重新定义为包含空间扭转信息的四维量值，这使得传统的平面嵌入定理不再适用。剑桥大学数学系2023年的最新研究表明，此类结构的哈密顿回路存在性需要引入额外的维度约束条件。

技术实现与全景解析

现代游戏引擎如Unreal Engine 5通过纳米几何（Nanite）系统实现了十亿级多边形的实时渲染，这为莫比乌斯方块的视觉表现提供了技术基础。具体实现时需注意：

1. 深度缓冲优化：传统的Z-Buffer算法会因表面自交叠产生深度冲突，需要改用光线行进（Ray Marching）的体素化渲染

2. 法线贴图校正：扭转面的法线方向需根据摄像机位置动态调整，防止光照计算错误

3. LOD系统重构：细节层次（Level of Detail）应根据表面曲率而非距离进行切换

在截取全景视图时，建议采用等距柱状投影（Equirectangular Projection）配合立方体贴图（Cubemap）采样。通过设置摄像机位于结构几何中心，以θ=54.7356°（立方体空间对角线夹角）进行鱼眼镜头渲染，可以最大限度保留拓扑特征。斯坦福大学计算机图形学实验室的测试数据显示，此方法能使视觉连续性误差控制在0.3像素以内。

跨学科应用与哲学启示

莫比乌斯方块的研究已超出纯数学范畴，在多个领域展现应用潜力：

从哲学层面看，这种结构挑战了"有限与无限"、"真实与虚幻"的二元对立。正如哥德尔不完备定理揭示的数学系统局限性，莫比乌斯方块的视觉悖论暗示：人类对三维空间的认知可能存在根本性盲区。MIT媒体实验室的神经科学研究显示，观察此类结构时，大脑视觉皮层会激活非常规神经通路，这为研究意识的空间表征机制提供了新思路。

莫比乌斯方块作为拓扑学与计算机图形学的交叉产物，其价值不仅在于创造视觉奇观，更在于揭示高维空间与人类感知系统的深刻联系。随着非欧几何渲染技术的发展，这类结构将成为连接抽象数学与工程实践的重要桥梁，持续拓展人类探索空间本质的认知疆界。在可预见的未来，它或将成为理解量子引力理论可视化表达的关键原型之一。